反向传播（二）

如何让多层神经网络学习呢？我们已了解了使用梯度下降来更新权重，反向传播算法则是它的一个延伸。要使用梯度下降法更新隐藏层的权重，你需要知道各隐藏层节点的误差对最终输出的影响。每层的输出是由两层间的权重决定的，两层之间产生的误差，按权重缩放后在网络中向前传播。既然我们知道输出误差，便可以用权重来反向传播到隐藏层。

我们已经知道一个权重的更新可以这样计算：

$$\Delta w_{i} = \eta\delta_j x_i$$

这里 $\delta$(error term) 是指：

$$\delta_j = (y_j-\hat{y_j})f^\prime(h_j) = (y_j-\hat{y_j})f^\prime_j(\sum_{}w_ix_i)$$

上面公式中 $(y_j-\hat{y_j})$ 是输出误差，激活函数 $f(h_j)$ 的导函是 $f^\prime(h_j)$ ，我们把这个导函数称做输出的梯度。

网上反向传播的版本很多，看千百个版本不如自己手推一个版本。

定义

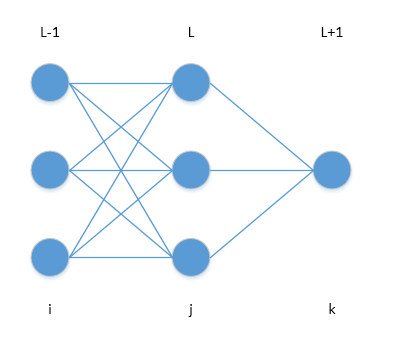
• 层 - 用带括号的字母L表示层，(L)表示第L层，(L-1)表示第L-1层，也就是L层的上一层，(L+1)表示第L+1层，也就是L层的下一层。
• 下标 - 用 i ，j ， k ，分别表示第 L-1 层的任意节点，第 L 层的任意节点，以及第 L+1 层的任意节点。
• $a^{(L)}_i$ - 表示节点 i 在第 L 层的输出。
• $w^{(L)}_{ij}$ - 表示在节点 i 和节点 j之间的权重，它代表第 L 层的权重。
• $o^{(L)}_i$ - 表示节点 i 在第 L 层的输出。
• $r^{(L)}$ - 表示第 L 层的节点数量
• $b^{(L)}_{i}$ - 表示节点 i 在第 L 层的偏差
• $\sigma()$ - 表示激活函数 sigmoid
  

前置条件

本文的的激活函数不再用 f(x) 表示，而用 sigmoid 函数作为激活函数，表示为 $\sigma()$。

为了进一步简化，对于节点 j 在第 L 层 的偏差 $b^{(L)}_{j}$ 将被合并到权重中，表示为 $w^{(L)}_{0j}$：

$$w^{(L)}_{0j} = b^{(L)}_j$$

那么节点 j 的输出：

$$a^{(L)}_j = b^{(L)}_j + \sum^{r^{(L-1)}}_{i=1} w^{(L)}_{ij}o^{(L-1)}_i = \sum^{r^{(L-1)}}_{i=0} w^{(L)}_{ij}o^{(L-1)}_i$$

误差函数

我们依然用 SSE 作为衡量预测结果的标准：

$$E = \frac{1}{2}(y - \hat{y})^2$$

误差偏导

反向传播算法的推导通过将链式法则应用于误差函数偏导开始：

$$\frac{\alpha E}{\alpha w^{(L)}_{ij}} = \frac{\alpha E}{\alpha a^{(L)}_{j}}\frac{\alpha a^{(L)}_j}{\alpha w^{(L)}_{ij}}$$

误差项依然用 $\delta$ 表示，不同的是带了上下标，表示节点 j 在第 L 层的误差项：

$$\delta^{(L)}_j =\frac{\alpha E}{\alpha a^{(L)}_{j}}$$

而

$$a^{(L)}_j = \sum^{r^{(L-1)}}_{i=0}w^{(L)}_{ij}o^{(L-1)}_i$$

$o^{(L-1)}_i$ 表示节点 i 在第 L-1 层的输出，求偏导可知：

$$\frac{\alpha a^{(L)}_j}{\alpha w^{(L)}_{ij}} = o^{(L-1)}_i$$

因此

$$\frac{\alpha E}{\alpha w^{(L)}_{ij}} = \delta^{(L)}_jo^{(L-1)}_i$$

输出层

这里我们假设输出层只有一个节点，因此节点的下标是1而不是 k ，那么最后一层的输出表示为$a^{(L+1)}_1$，由误差函数可知：

$$E = \frac{1}{2}(y - \hat{y})^2 = \frac{1}{2}(y-\sigma(a^{(L+1)}_1))^2$$

$\sigma()$ 是激活函数 sigmoid 函数。同样令输出层的误差项为 $\delta^{(L+1)}_1 = \frac{\alpha E}{\alpha a^{(L+1)}_{1}}$，所以

$$\delta^{(L+1)}_1 = \frac{\alpha E}{\alpha a^{(L+1)}_{1}} = -(y-\sigma(a^{(L+1)}_1))\sigma^\prime(a^{(L+1)}_1) = -(y-\hat{y})\sigma^\prime(a^{(L+1)}_1)$$

隐藏层

对于隐藏层节点 j 的误差项：

$$\delta^{(L)}_j = \frac{\alpha E}{\alpha a^{(L)}_{j}} = \sum^{r^{(L+1)}}_{k=1}\frac{\alpha E}{\alpha a^{(L+1)}_{k}}\frac{\alpha a^{(L+1)}_k}{\alpha a^{(L)}_j}$$

上式公式中为什么要求和？请看下图：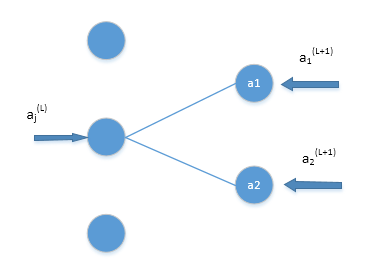

因为激活值可以通过不同的途径影响代价函数(误差函数)，也就是说神经元一边通过 $a^{(L+1)}_1$ 来影响代价函数，另一边通过 $a^{(L+1)}_2$ 来影响代价函数，得把这些都加起来。至于求和公式中 k 是从1开始的，因为输出层没有偏差，只有输出节点，而从0开始表示该层包含一个偏差的节点。

令 $\delta^{(L+1)}_k = \frac{\alpha E}{\alpha a^{(L+1)}_{k}}$ ，所以

$$\delta^{(L)}_j = \sum^{r^{(L+1)}}_{k=1}\delta^{(L+1)}_k\frac{\alpha a^{(L+1)}_k}{\alpha a^{(L)}_j}$$

由于

$$a^{(L+1)}_k = \sum^{r^{(L)}}_{j=0}w^{(L+1)}_{jk}\sigma(a^{(L)}_j)$$

所以

$$\frac{\alpha a^{(L+1)}_k}{\alpha a^{(L)}_j} = w^{(L+1)}_{jk}\sigma^\prime(a^{(L)}_j)$$

因此

$$\delta^{(L)}_j = \sum^{r^{(L+1)}}_{k=1}\delta^{(L+1)}_kw^{(L+1)}_{jk}\sigma^\prime(a^{(L)}_j) = \sigma^\prime(a^{(L)}_j)\sum^{r^{(L+1)}}_{k=1}w^{(L+1)}_{jk}\delta^{(L+1)}_k$$

最后带入公式

$$\frac{\alpha E}{\alpha w^{(L)}_{ij}} = \delta^{(L)}_jo^{(L-1)}_i = \sigma^\prime(a^{(L)}_j)o^{(L-1)}_i\sum^{r^{(L+1)}}_{k=1}w^{(L+1)}_{jk}\delta^{(L+1)}_k$$

至此，反向传播推导就结束了。

总结

上面推导出了很多公式，总结一下对我们有用的公式：

• 误差函数对权重的偏导，可以理解为代价函数（误差）对权重 w 的微小变化有多敏感
  $\frac{\alpha E}{\alpha w^{(L)}_{ij}} = \delta^{(L)}_jo^{(L-1)}_i$
• 输出层的误差项
  $\delta^{(L+1)}_1 = -(y-\hat{y})\sigma^\prime(a^{(L+1)}_1)$
• 隐藏层误差项
  $\delta^{(L)}_j = \sigma^\prime(a^{(L)}_j)\sum^{r^{(L+1)}}_{k=1}w^{(L+1)}_{jk}\delta^{(L+1)}_k$

例子

import numpy as np
from data_prep import features, targets, features_test, targets_test

np.random.seed(21)

def sigmoid(x):
    """
    Calculate sigmoid
    """
    return 1 / (1 + np.exp(-x))


# 超参数
n_hidden = 2  # number of hidden units
epochs = 900
learnrate = 0.005

n_records, n_features = features.shape
last_loss = None
# 初始化权重
weights_input_hidden = np.random.normal(scale=1 / n_features ** .5,
                                        size=(n_features, n_hidden))
weights_hidden_output = np.random.normal(scale=1 / n_features ** .5,
                                         size=n_hidden)
print('weights_input_hidden={}'.format(weights_input_hidden))
print('weights_hidden_output={}'.format(weights_hidden_output))
for e in range(epochs):
    del_w_input_hidden = np.zeros(weights_input_hidden.shape)
    del_w_hidden_output = np.zeros(weights_hidden_output.shape)

    for x, y in zip(features.values, targets):
        ## 前向传播 ##
        # TODO: 计算输出
        #print('x={}'.format(x))
        hidden_input = np.dot(x, weights_input_hidden)
        hidden_output = sigmoid(hidden_input)
        output = sigmoid(np.dot(hidden_output, weights_hidden_output))

        ## 后向传播 ##
        # TODO: 实际值与期望的差值
        error = y - output

        # TODO: 对输出求误差梯度
        output_error_term = error * output * (1-output)

        ## 传播误差到隐藏层

        # TODO: 计算隐藏层对误差的贡献
        hidden_error = np.dot(weights_hidden_output, output_error_term)

        # TODO: 对隐藏层求误差梯度
        hidden_error_term = hidden_error * hidden_output * (1-hidden_output)

        # TODO: 更新权重的变化率
        del_w_hidden_output += output_error_term * hidden_output
        del_w_input_hidden += hidden_error_term * x[:, None]

    # TODO: 更新权重
    weights_input_hidden += learnrate * del_w_input_hidden / n_records
    weights_hidden_output += learnrate * del_w_hidden_output / n_records

    # 打印训练集上的均方差
    if e % (epochs / 10) == 0:
        hidden_output = sigmoid(np.dot(x, weights_input_hidden))
        out = sigmoid(np.dot(hidden_output,
                             weights_hidden_output))
        loss = np.mean((out - targets) ** 2)

        if last_loss and last_loss < loss:
            print("Train loss: ", loss, "  WARNING - Loss Increasing")
        else:
            print("Train loss: ", loss)
        last_loss = loss

# 对测试数据计算准确度
hidden = sigmoid(np.dot(features_test, weights_input_hidden))
out = sigmoid(np.dot(hidden, weights_hidden_output))
predictions = out > 0.5
accuracy = np.mean(predictions == targets_test)
print("Prediction accuracy: {:.3f}".format(accuracy))

参考文献

• Brilliant-Backpropagation
• 反向传播的微积分原理