反向传播（一）

反向传播是神经网络的基石，它的名字也很容易理解，因为梯度的计算是通过网络向后进行，首先计算最终权重层的梯度，并且最后计算第一层权重的梯度。在计算前一层梯度时，重复使用来自上一层梯度的计算部分。这种误差信息的向后流动就形象的称为反向传播。

链式法则

首先介绍下链式法则，他是反向传播的核心，链式法则也即复合函数求导的过程。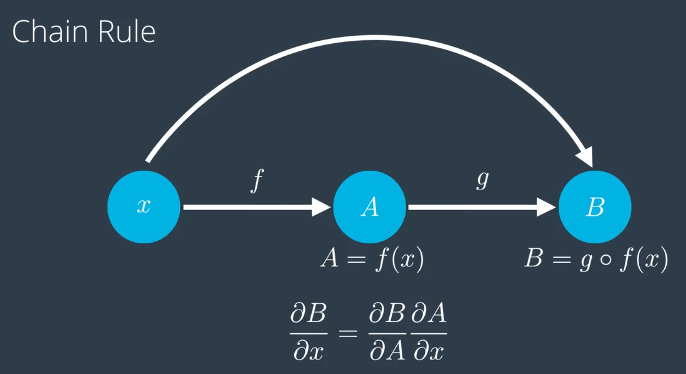

链式法则的内容是：如果有一个变量 x ，以及一个关于 x 的函数 f(x) 我们将简称为 A ，另一个函数 g ，将 f(x) 作为 g 的变量得到 g o f(x) 。链式法则证明： B 关于 x 的偏导数，就是 B 关于 A 的偏导数，乘以 A 关于 x 的偏导数，所以对复合函数求导就是一系列导数的乘积。

SSE

怎么样衡量预测结果的标准？最简单，最容易想到的是用实际目标值 y 减去网络输出值 ŷ ，以两者差值衡量误差。

$$E = y - \hat{y}$$

然而，若预测值高于目标值，那么差值就为负数，若预测值低于目标值，差值为正数，我们希望误差能够保持符号一致，要让符号全部归正，可以求差值的平方：

$$E = (y - \hat{y})^2$$

你可能在想，为什么不直接用绝对值呢？问得好！这是因为使用平方值时，异常数值会被赋予更高的惩罚值，而较小误差的惩罚值则较低。

目前我们仅得到单次预测的误差，我们希望求出全体数据的整体误差，那么可以对每项数据 μ 的误差求和:

$$E = \sum_{μ}(y - \hat{y})^2$$

最后我们在式子前面加上$\frac{1}{2}$，以便简化后续计算。怎么个简化法？这是为了后面求导时可以跟平方数抵消，那么最后的公式：

$$E = \frac{1}{2}\sum_{μ}(y - \hat{y})^2$$

此公式通常称为误差平方和，简称 SSE(sum of the squared errors)。误差平方和，可用于衡量神经网络的预测效果，值越高，预测效果越差，值越低，预测效果越好，这也是刚才我们求完差值后为什么用平方而不是取绝对值的原因。

梯度下降

这里举一个简化的例子来阐述梯度下降的过程，我们只考虑单行数据的情况。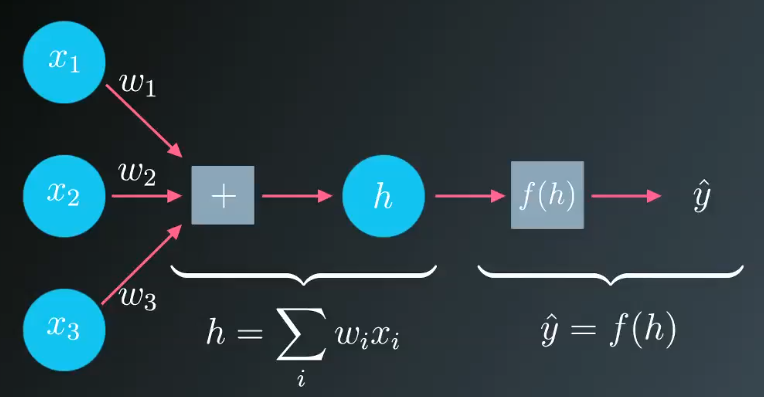

上面SSE的公式中全体数据用 μ 表示，我们可以将这些数据看成两组表格、数组或者矩阵,其中一组包含输入值，另一组包含目标值 y ，每项数据占一行位置 μ = 1 表示第一行数据，如果需要计算整体误差，可以逐行计算误差平方和，然后对所得结果求和。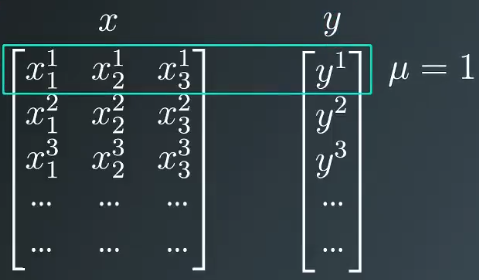

我们将数据带入到公式中：

$$E = \frac{1}{2}(y - \hat{y})^2 = \frac{1}{2}(y - f(\sum_{i}w_ix_i))^2$$

展开预测值之后，可以看出权重是误差函数的参数，我们的目标是求取能使误差最小化的权重值，如下图：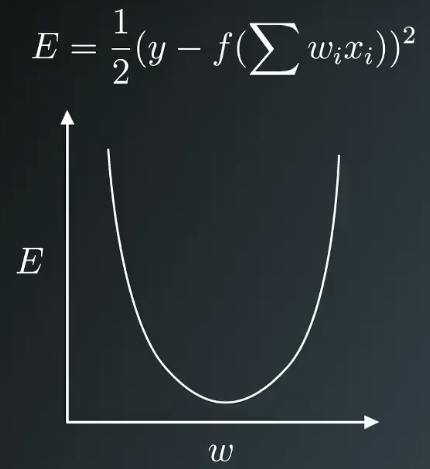

由上图知，我们的目标就是求取图形碗底对应的权值，从某个随机权值出发，逐步向误差最小值的方向前进，这个方向与梯度（斜率）相反，只要始终沿着梯度反复逐步下降，最终能求得对应最小误差的权值，这就是梯度下降的过程。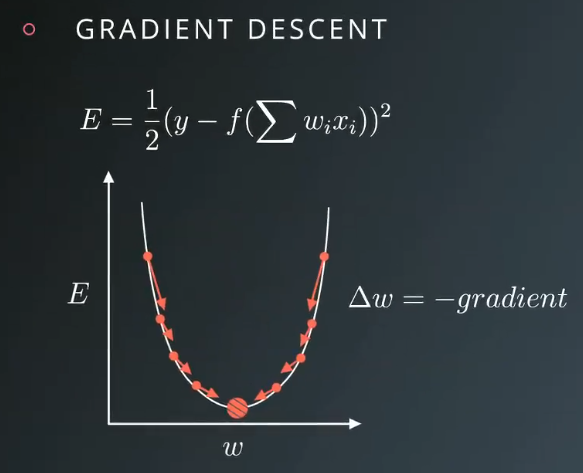

下面来更新权值，新的权值 $w_i$ 等于旧的权值 $w_i$ 加上更新步长$\Delta w_i$：

$$w_i = w_i + \Delta w_i$$

由于前述更新步长与梯度成正比，而梯度等于误差关于每个权重$w_i$的偏导数：

$$\Delta w_i \propto -\frac{\alpha E}{\alpha w_i}$$

公式中还需添加一个缩放系数变量用来控制梯度下降中更新步长的大小：

$$\Delta w_i = -\eta\frac{\alpha E}{\alpha w_i}$$

这个变量叫作学习速率用希腊字母 $\eta$ 表示。对于计算梯度需要用到多元微积分，也就是前面提到的链式法则。下面我们展开计算梯度：

$$\frac{\alpha E}{\alpha w_i} = \frac{\alpha}{\alpha w_i}\frac{1}{2}(y-\hat{y})^2 = \frac{\alpha}{\alpha w_i}\frac{1}{2}(y-\hat{y}(w_i))^2$$

鉴于输出值 $\hat{y}$ 是权重的函数，这里相当于复合函数，可以通过链式法则来求偏导，前面已经介绍过了，那么：

$$\frac{\alpha E}{\alpha w_i} = (y-\hat{y})\frac{\alpha}{\alpha w_i}(y-\hat{y}) = -(y-\hat{y})\frac{\alpha \hat{y}}{\alpha w_i}$$

下面再来对 $\hat{y}$ 求偏导，我们知道

$$\hat{y} =f(h)$$

而

$$h = \sum_{i}w_ix_i$$

因此

$$\frac{\alpha E}{\alpha w_i} = -(y-\hat{y})f^\prime(h)\frac{\alpha}{\alpha w_i}\sum_{i}w_ix_i$$

我们把上式的最后一项单独提出来，在求和式子中，每个权重仅是单个子项的参数：

$$\frac{\alpha}{\alpha w_i}\sum_{i}w_ix_i$$

将其展开

$$\frac{\alpha}{\alpha w_i}\sum_{i}w_ix_i = \frac{\alpha}{\alpha w_i}[w_1x_1+w_2x_2+...+w_nx_n] = x_i+0+0+0+...$$

综合来看，误差平方关于 $w_i$ 的偏导数等于
$\frac{\alpha E}{\alpha w_i} = -(y-\hat{y})f^\prime(h)x_i$
所以

$$\Delta w_i = \eta(y-\hat{y})f^\prime(h)x_i$$

最后我们得出结论，更新步长就等于学习速率 $\eta$ 乘以预测差值，乘以激活函数导数，再乘以输入值，为方便后续应用，我们将预测差值乘以激活函数的导数用小写字母 $\delta$ 表示

$$\delta = (y-\hat{y})f^\prime(h)$$

那么权值更新公式可以重新写为
$w_i = w_i+\eta\delta x_i$
以上便是单行数据的情况，你的神经网络中可能会有多个输出单元，可以将其视为单个输出网络的堆叠架构，但需将输入单元连接到新的输出单元，这时整体误差等于每个输出单元的误差之和。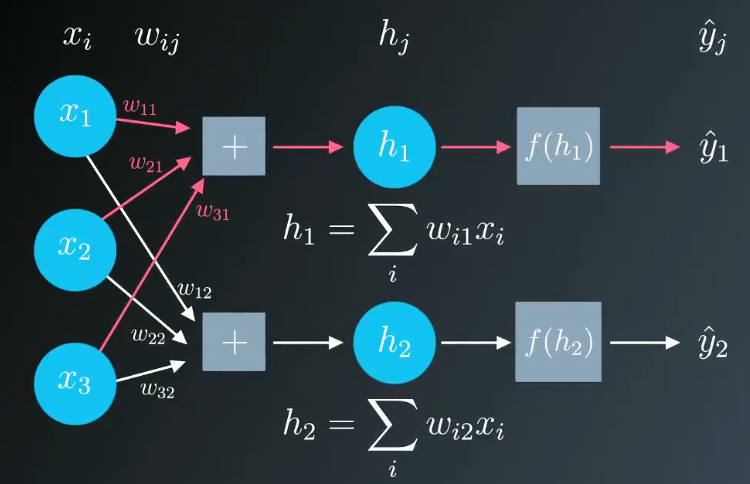

梯度下降法可以扩展适用于这种情况，只需分别计算每个输出单元的误差项
$\delta_j = (y_j-\hat{y}_j)f^\prime(h_j)$
$\Delta w_{ij} = \eta\delta_jx_i$
以上便是反向传播的核心知识点，下一章，对反向传播进行数学推导。