前向传播

前向传播是神经网络用来将输入变成输出的流程。

输入层->隐藏层

在下面这个简单的网络图中，输入单元被标注为 $x_{_1}$​，$x_{_2}$​，$x_{_3}$​，隐藏层节点是 $h_{_1}$​，$h_{_2}$。

这个网络图中有多个输入单元和多个隐藏单元，它们的权重需要有两个索引 $w_{_{ij}}$​，其中 i 表示输入单元，j 表示隐藏单元。

为了定位权重，我们把输入节点的索引 i 和隐藏节点的索引 j​ 结合，得到：
$w_{_{11}}$ - 代表从 $x_{_1}$​ 到 $h_{_1}$​ 的权重；
$w_{_{12}}$ - 代表从 $x_{_1}$ 到 $h_{_2}$ 的权重。
…

下图包括了从输入层到隐藏层的所有权重，用 $w_{_{ij}}$​ 表示：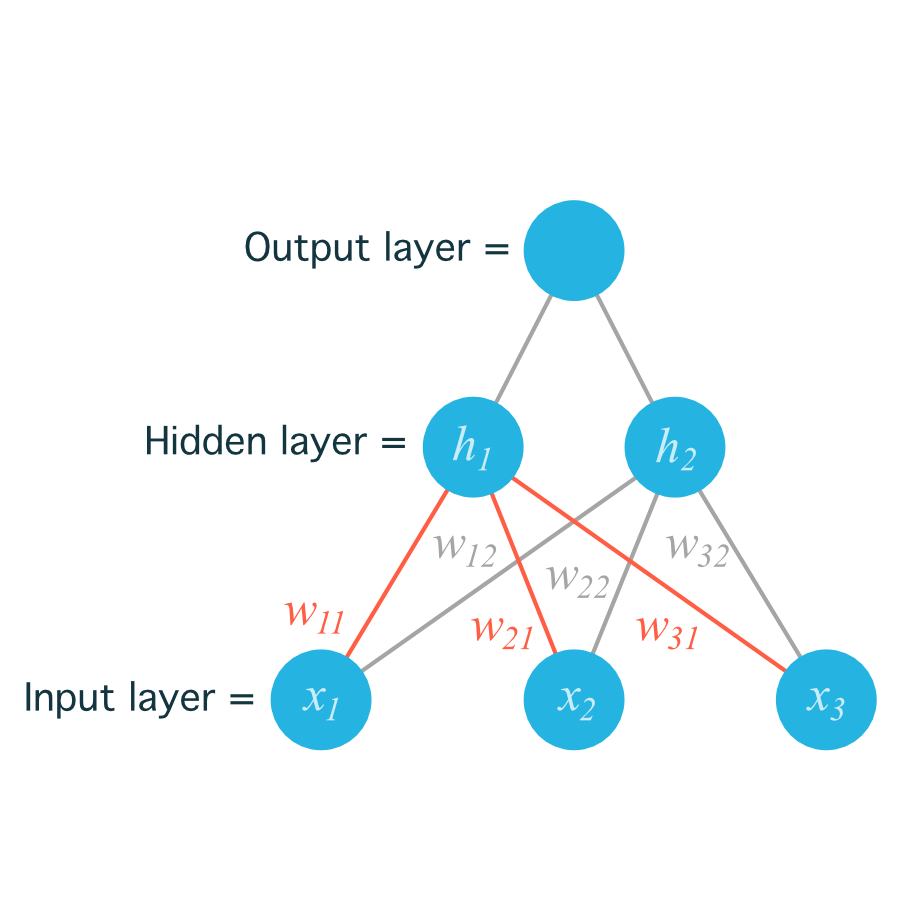

现在，将权重储存在矩阵中，由 $w_{_{ij}}$​ 来索引。矩阵中的每一行对应从同一个输入节点发出的权重，每一列对应传入同一个隐藏节点的权重。这里我们有三个输入节点，两个隐藏节点，权重矩阵表示为：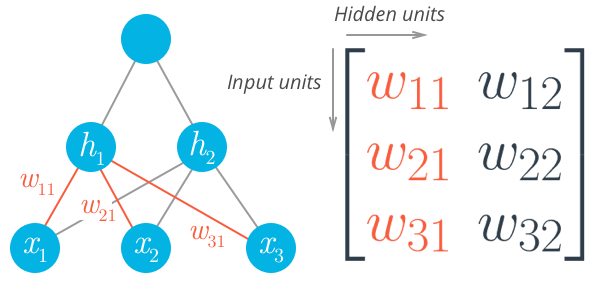

运用矩阵乘法可以得出每一个隐藏层节点 $h_{_j}$：

$$h_{_j} = \sum_{i}x_{_i}w_{_{ij}}$$

那么：

$$h_{_1} = x_{_1}w_{_{11}} + x_{_2}w_{_{21}} + x_{_3}w_{_{31}}$$

以此类推，可以求出第二个隐藏节点$h_{_2}$：

$$h_{_2} = x_{_1}w_{_{12}} + x_{_2}w_{_{22}} + x_{_3}w_{_{32}}$$

在 NumPy 中，我们可以直接使用 np.dot：
hidden_inputs = np.dot(inputs, weights_input_to_hidden)

上面的网络图是不含偏差的，实际上加上偏差的网络图前向传播是类似的: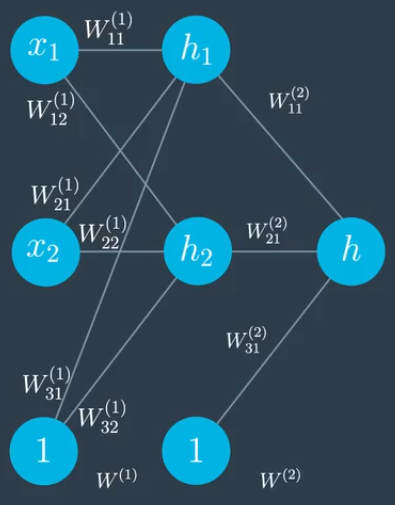

如上图具有上标(1)的权重属于第一层，具有上标(2)的权重属于第二层级，偏差不再叫b，现在叫做 $W_{31}$， $W_{_{32}}$ 等等。

在第一层级中，我们执行前向传播可以得出：

$$h_1 = W^{^{(1)}}_{_{11}}x_{_1} + W^{^{(1)}}_{_{21}}x_{_2} + W^{^{(1)}}_{_{31}}$$ $$h_2 = W^{^{(1)}}_{_{12}}x_{_1} + W^{^{(1)}}_{_{22}}x_{_2} + W^{^{(1)}}_{_{32}}$$

我们再给每层加上一个激活函数，选定 sigmoid 函数为我们的激活函数。先简单介绍下 sigmoid 函数。

sigmoid 函数

sigmoid 函数是一个有着优美S形曲线的数学函数，在逻辑回归、人工神经网络中有着广泛的应用。它的数学形式：

$$\sigma(x) = \frac{1}{1+e^{-x}}$$

其函数图像如下：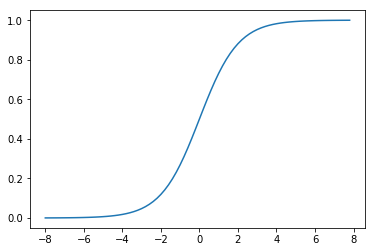

可以看出，sigmoid 函数连续，光滑，严格单调，以(0,0.5)中心对称，是一个非常良好的阈值函数。sigmoid 函数的值域范围限制在(0,1)之间，我们知道[0,1]与概率值的范围是相对应的，这样sigmoid函数就能与一个概率分布联系起来了。

sigmoid 函数的导数

sigmoid 函数有一个美丽的导数，我们可以在下面的计算中看到。这将使我们的反向传播步骤更加简洁，这也是这里为什么选用它为激活函数的原因。

$$\sigma^{'}(x) = \frac{\alpha}{\alpha x}\frac{1}{1+e^{-x}} = \frac{e^{-x}}{(1+e^{-x})^2} = \frac{1}{1+e^{-x}}\frac{e^{-x}}{1+e^{-x}} = \sigma(x)(1-\sigma(x))$$

隐藏层节点通过 sigmoid 激活函数可以分别求得隐藏层的输出为:
hide_out_1 = $\sigma(h_1)$
hide_out_2 = $\sigma(h_2)$

隐藏层->输出层

通过线性方程，结合隐藏层的输出可以求出输出节点：

$$h = W^{^{(2)}}_{_{11}}\sigma(h_1) + W^{^{(2)}}_{_{21}}\sigma(h_2) + W^{^{(2)}}_{_{31}}$$

对输出节点应用 sigmoid 函数，得出预测：

$$\hat{y} = \sigma(h)$$

即在 0 到 1 之间的概率 用 ŷ 表示。至此，前向传播就结束了。