神经网络的维度是个经常让人迷糊的概念，本文以卷积神经网络为例介绍怎么计算维度。文中的公式也可以作为知识点backup。

维度

先来个例子，按以下步骤用Keras创建一个简单的CNN。

首先创建一个序列模型，使用add() 方法向网络中添加层级：

from keras.models import Sequential
from keras.layers import Conv2D

model = Sequential()
model.add(Conv2D(filters=16, kernel_size=2, strides=2, padding='valid',
    activation='relu', input_shape=(200, 200, 1)))
model.summary()

让我们通过该网络所提供的参数研究卷积层的维度如何变化，你可以在jupyter notebook上运行。现在来看看输出结果是什么：

summary_result
结果显示该卷积层有80个参数，对应的输出在Param #。同时注意卷积层的形状是如何变化，对应输出内容中的Output Shape,上图中，None对应的是批次大小，卷积层的高度为100，宽度为100，深度为16。

本文以Keras来搭建卷积网络，让我们先来了解下卷积层（Conv2D）的参数。

Conv2D

keras.layers.convolutional.Conv2D(filters,
                                  kernel_size,
                                  strides=(1, 1),
                                  padding='valid',
                                  data_format=None,
                                  dilation_rate=(1, 1),
                                  activation=None,
                                  use_bias=True,
                                  kernel_initializer='glorot_uniform',
                                  bias_initializer='zeros',
                                  kernel_regularizer=None,
                                  bias_regularizer=None,
                                  activity_regularizer=None,
                                  kernel_constraint=None,
                                  bias_constraint=None)

二维卷积层，即对图像的空域卷积。该层对二维输入进行滑动窗卷积，当使用该层作为第一层时，应提供input_shape参数。例如input_shape = (128,128,3)代表128*128的彩色RGB图像（data_format=’channels_last’）

参数

filters：卷积核的数目（即输出的维度）
kernel_size：单个整数或由两个整数构成的list/tuple，卷积核的宽度和长度。如为单个整数，则表示在各个空间维度的相同长度。
strides：单个整数或由两个整数构成的list/tuple，为卷积的步长。如为单个整数，则表示在各个空间维度的相同步长。任何不为1的strides均与任何不为1的dilation_rate均不兼容
padding：补0策略，为“valid”, “same” 。“valid”代表只进行有效的卷积，即对边界数据不处理。“same”代表保留边界处的卷积结果，通常会导致输出shape与输入shape相同。
activation：激活函数，为预定义的激活函数名（参考激活函数），或逐元素（element-wise）的Theano函数。如果不指定该参数，将不会使用任何激活函数（即使用线性激活函数：a(x)=x）
dilation_rate：单个整数或由两个个整数构成的list/tuple，指定dilated convolution中的膨胀比例。任何不为1的dilation_rate均与任何不为1的strides均不兼容。
data_format：字符串，“channels_first”或“channels_last”之一，代表图像的通道维的位置。该参数是Keras 1.x中的image_dim_ordering，“channels_last”对应原本的“tf”，“channels_first”对应原本的“th”。以128x128的RGB图像为例，“channels_first”应将数据组织为（3,128,128），而“channels_last”应将数据组织为（128,128,3）。该参数的默认值是~/.keras/keras.json中设置的值，若从未设置过，则为“channels_last”。
use_bias:布尔值，是否使用偏置项
kernel_initializer：权值初始化方法，为预定义初始化方法名的字符串，或用于初始化权重的初始化器。参考initializers
bias_initializer：权值初始化方法，为预定义初始化方法名的字符串，或用于初始化权重的初始化器。参考initializers
kernel_regularizer：施加在权重上的正则项，为Regularizer对象
bias_regularizer：施加在偏置向量上的正则项，为Regularizer对象
activity_regularizer：施加在输出上的正则项，为Regularizer对象
kernel_constraints：施加在权重上的约束项，为Constraints对象
bias_constraints：施加在偏置上的约束项，为Constraints对象

详细了解这些参数，建议参阅官方文档。下图表示3*3、stride为1的卷积：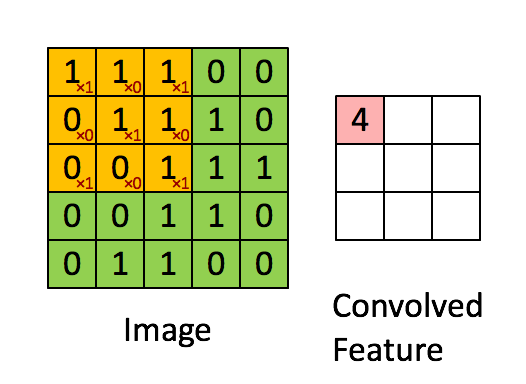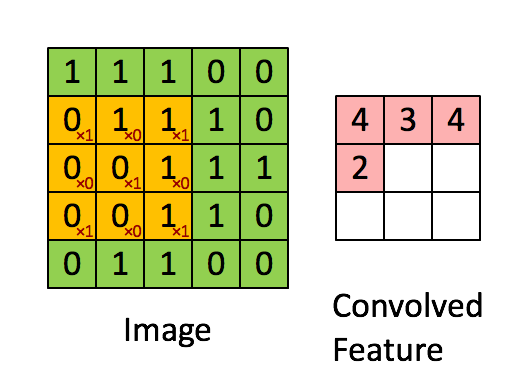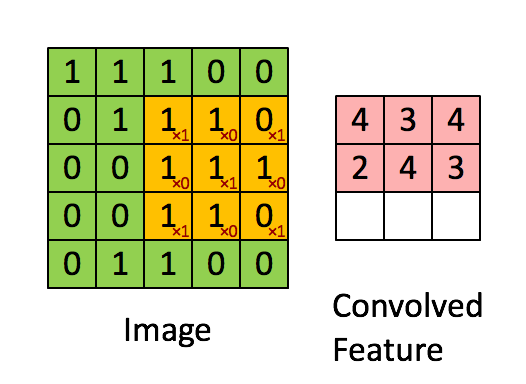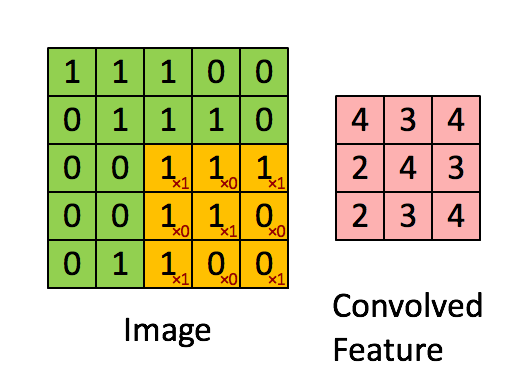
conv2D

卷积层中的参数数量

我们的卷积层中参数数量取决于 filters、kernel_size 和 input_shape 的值。这里定义几个变量：

K - 卷积层中的过滤器数量
F - 卷积过滤器的高度和宽度
D_in - 上一层级的深度

注意：K = filters，F = kernel_size。类似地，D_in 是 input_shape 元祖中的最后一个值。
因为每个过滤器有 F*F*D_in 个权重，卷积层由 K 个过滤器组成，因此卷积层中的权重总数是 K*F*F*D_in。因为每个过滤器有 1 个偏差项，卷积层有 K 个偏差。因此，卷积层中的参数数量是 K*F*F*D_in+K。

卷积层的形状

卷积层的形状取决于 kernel_size、input_shape、padding 和 stride 的值。我们定义几个变量：

K - 卷积层中的过滤器数量
F - 卷积过滤器的高度和宽度
H_in - 上一层级的高度
W_in - 上一层级的宽度

注意：K = filters、F = kernel_size，以及S = stride。类似地，H_in 和 W_in 分别是 input_shape 元祖的第一个和第二个值。

卷积层的深度始终为过滤器数量 K。

如果 padding = ‘same’，那么卷积层的空间维度如下：

height = ceil(float(H_in) / float(S))
width = ceil(float(W_in) / float(S))

如果 padding = ‘valid’，那么卷积层的空间维度如下:

height = ceil(float(H_in - F + 1) / float(S))
width = ceil(float(W_in - F + 1) / float(S))

练习

from keras.models import Sequential
from keras.layers import Conv2D

model = Sequential()
model.add(Conv2D(filters=32, kernel_size=3, strides=2, padding='same',
    activation='relu', input_shape=(128, 128, 3)))
model.summary()

习题1

该卷积层有多少个参数？
A.902
B.306
C.896
D.1034

答案：(32 x 3 x 3 x 3) + 32 = 896

习题2

卷积层的深度是多少？
A.3
B.16
C.32
D.64

答案：卷积层的深度始终等于过滤器的数量32。

习题2

卷积层的宽度是多少？
A.3
B.16
C.32
D.64

答案：64

总结

卷积神经的维度跟参数密切相关，Conv2D这个接口的参数很多，但是每个参数都有不同的作用。最后总结下通常用的比较多参数：

filters - 过滤器数量。过滤器数量和每个过滤器的大小控制卷积层的行为。
kernel_size - 指定（方形）卷积窗口的高和宽的数字，可表示为数字或元组。

你可能还需要调整其他可选参数：

strides - 卷积 stride ，指过滤器滑过图片的数量。如果不指定任何值，则 strides 设为 1，可表示为数字或元组。
padding - 选项包括 ‘valid’ 和 ‘same’。如果不指定任何值，则 padding 设为 ‘valid’。
activation - 通常为 ‘relu’。如果未指定任何值，则不应用任何激活函数。强烈建议你向网络中的每个卷积层添加一个 ReLU 激活函数。

在模型中将卷积层当做第一层级（出现在输入层之后）时，必须提供另一个 input_shape 参数：

input_shape - 指定输入的高度、宽度和深度（按此顺序）的元组。